Understanding Critical Values: Explanation & Calculation

Understanding Critical Values: Explanation & Calculation

The critical value serves as the threshold that determines whether we accept or reject the null hypothesis in hypothesis testing. It's a specific point on a scale beyond which a researcher would reject the null hypothesis in favor of the alternative hypothesis.

Statisticians compare computed test statistics with these critical values to perform hypothesis testing. The null hypothesis is rejected if the computed statistic is greater than the crucial value since it suggests that the outcome is not likely to have happened by chance alone.

This article aims to cover how critical values are calculated, their significance in different statistical tests; and their practical applications in drawing meaningful conclusions from data analysis.

(toc)

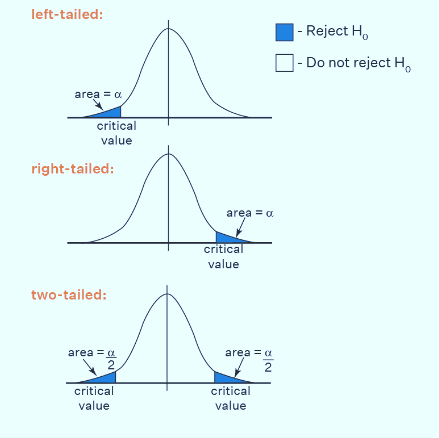
What is Critical Value?

There are critical values for various types of hypothesis tests. These values can be interpreted from the distribution of the test statistic and the significance level. One-tailed hypothesis tests have a single critical value; while two-tailed tests have two critical values.

Understanding the Critical Value: A Definition

A critical value is a threshold value used in hypothesis testing to determine whether the observed results are likely due to chance or reflect a real effect. It acts as a boundary line that separates the region of expected results from the region of unexpected results.

Determination:

·       Depends on two factors:

1.     Significance level (α): The maximum acceptable probability of rejecting the null hypothesis when it's true (false positive).

2.     Degrees of freedom: The amount of information available in the data.

·       Differs depending on the particular type of statistical test being employed.

Interpretation:

·       If the calculated test statistic falls beyond the critical value, then the null hypothesis is rejected and indicates a statistically significant effect.

·       If the test statistic falls within the critical value range, the null hypothesis remains accepted.

The formula for Calculating the Critical Value:

The formula for a critical value is based on the specific type of hypothesis test we’re conducting. Critical values for hypothesis testing can be calculated from either confidence intervals or significance levels. Critical value formulas are summarized below.

Determining Critical Values from Confidence Intervals:

Using the confidence interval, we can find the critical value for one and two-tailed tests. Imagine that a 95% confidence level has been selected for performing a hypothesis test. The critical value can be calculated as follows:

1.     Take 100% and deduct the chosen (95%) confidence level.

2.     Transform this value into decimals to obtain the value of α.

3.     The alpha level remains unchanged from the previous step for a one-tailed test.

4.     The alpha level is halved in the case of a two-tailed test.

5.     The critical value can be found by referencing the suitable distribution table based on the alpha value which varies according to the type of test performed.

Note:

• The detailed procedure for step 4 will be explained in the following sections.

Classification of critical value:

We've categorized critical values into three fundamental types that rely on the statistical test being conducted. Here are these primary types:

1.     T – Critical value

2.     Z – Critical value

3.     F – Critical value

1.   T – Critical Value:

 A t-test is applied in situations where the S.D (Standard deviation) of the population is unknown and the sample size is below 30. A t-test is performed when the population data follows a student’s t-distribution. The critical value for t can be computed in the following manner:

Step 1: Establish the α (level of significance).

Step 2: Deduct one from the size of the sample. This provides the value for degrees of freedom (df).

Step 3: If the hypothesis test aims at a particular direction, then refer to the one-tailed t-distribution table. In situations where the test extends both directions then refer to the two-tailed t - t-distribution table.

Step 4: Find the intersection between the degrees of freedom (displayed on the left side) and the alpha value (shown on the top row) in the table and that is the critical value.

The test statistic for a one-sample t-test is calculated as:

t = (x̄ - μ) / (s / √n)

Where:

·        x̄ is the sample mean

·        μ denoted the population mean.

·        s is the sample standard deviation

·        n is the sample size

The test statistic for a two-sample t-test: (x̄₁ - x̄₂) – (μ₁- μ₂) / √ (s₁²/n₁ + s₂²/n₂).

Decision-Making Criteria:

·        If the test statistic is greater than the t critical value (for a right-tailed hypothesis test) then reject the null hypothesis.

·        If the test statistic is less than the critical value (for a left-tailed hypothesis test) then reject the null hypothesis.

·        Reject the null hypothesis if the test statistic falls outside the acceptance region in a two-tailed hypothesis test.

This decision criteria applies universally to all tests. Only the test statistic and critical value vary depending on the specific test.

1.   Z – Critical value:

The z-test is used when the population standard deviation is known and the sample size is large (usually n > 30). The critical value of Z can be computed in the following manner:

·        Compute the level of α.

·        Deduct the level of α from one for a 2-tailed test. Deduct the level of alpha from 0.5 for the 1-tailed test.

·        Finding the area in the z distribution table will yield the z critical value. After the computation, the critical value for a left-tailed test must have a negative sign appended to it.

The Formula for one Sample Z test: z = (x̄ - μ) / (σ / √n)

The Formula for two Sample Z test: z = x̄₁ - x̄₂) – (μ₁- μ₂) / √ (σ₁²/n₁ + σ₂²/n₂).

2.   F – Critical value:

The F test is used for both variance comparison and regression analysis. The F critical value is computed as follows:

·        Set the level of alpha.

·        Minus one from the number of observations in the first sample gives you the first degree of freedom. Let's call it x.

·        Minus one from the 2^nd sample size to take the second degree of freedom. Let’s call it y.

·        With the f-distribution table, locate the cell where the column labeled with x and the row labeled with y intersect. This cell will contain the critical value of f.

Calculation of Critical Value:

Example

A researcher wants to assess if the average score of students on a test is higher than 75. A sample of 20 students has a mean score of 78 with a standard deviation of 5. The significance level (α) chosen is 0.05.

Solution:

Step 1:

Establish α = 0.05.

Step 2:

Degrees of freedom (df) = 20 - 1 = 19.

Step 3:

For a one-tailed test, refer to the t-distribution table. Critical t-value (for α = 0.05 and df = 19) ≈ 1.729.

Test statistic calculation: t = (78 - 75) / (5 / √20) ≈ 3 / 1.12 ≈ 2.68

Decision:

The calculated t-value (2.68) > critical value (1.729), indicates sufficient evidence to reject the null hypothesis that the average score is not greater than 75.

Conclusion:

This article explored the critical value of hypothesis testing, its definition, and its role in different statistical tests. We learned how to calculate critical values for various scenarios and how they help us make decisions about rejecting or accepting the null hypothesis.