Standard Deviation (SD): Definition, Formulas, & Examples

standard-deviation-sd-definition-formulas-and-examples

Standard Deviation (SD) is a significant statistical term. It plays a crucial role to measure the dispersion of datasets in real-life problems in several industrial sectors, population departments, insurance companies, engineering, etc.

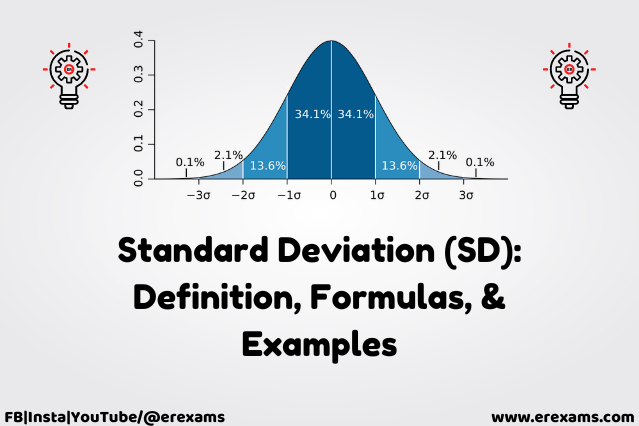
The standard deviation shows how many variations there are from the mean and gives an idea of the shape of the distribution. Standard deviation and variance both terms are interconnected to each other similar to the square and square root of a number.

The variance combines all the data values in a data set to give a measure of a data’s spread about its mean. SD measures how far, on average, each data value differs from the average (mean). In this blog, we will discuss the term standard deviation, its formula, some useful properties, and examples.

What is a Standard Deviation (SD):

When we take the square root of the variance, we get the value called standard deviation (SD). SD is the mensuration of how spread out the data is. SD has the measuring units the same as the units of the data set/point.  SD is the square root of the sum of the squared distances from the mean of data values.

Formula of Standard Deviation:

Since standard deviation and variance are interlinked terms and the variance is calculated by taking the mean (average) of the squares of difference b/w each data value and the mean, so by taking the square root of variance end up with a number that is more easily comparable to the original data in the list. Mathematically,

σ = √[∑(x−x̄)² /n]

If we take a square of the above expression i.e. σ² = (∑x−x̄)²/n).

Which represents the term variance that gives a mean average of the squared distance b/w each data point and the mean.

Here x̄ is the average (mean) of the data sets. Now we will elaborate on some important properties of the standard deviation that play a vital role to get insights from the data sets.

Properties of Standard Deviation:

·       SD is only used to measure the spread or dispersion of a data set around the mean (average).

·       Standard deviation is never negative because it is an average of the squared distances (x−x̄)².

·       SD is sensitive to an outlier value in the given data sets/pints. Even a single outlier can elevate (raise) the SD value and in turn, wring (deform) the picture of the expansion or dispersion.

·       For data with approximately the same mean, the greater the spread, the greater the standard deviation.

·       A low standard deviation (SD) shows that the data points tend to be closer to the mean than a larger standard deviation.

Method to Compute SD:

It is very important to apprehend how to calculate the standard deviation of the given data as this term is very frequently used in our life. Here we will elaborate to calculate SD from the given data.

Step 1: First of all find out the mean (average) of the given data which is equivalent to some of the observations divided by the number of the observations

x̄ = ∑x /n

Step 2: Compute the difference (x - x̄) for each term of the given data set.

Step 3: Square all the values computed in step 2 i.e. (x - x̄)².

Step 4: Now sum up all the values computed in step 3 i.e. ∑(x - x̄)².

Step 5: Dived this cumulative value (∑(x - x̄)2) by the total number of observations i.e. (∑x−x̄)2/n) which is the variance (σ2).

Step 6: In the last step, you only need to take the square root of the variance i.e. σ = √[∑(x−x̄)2 /n] which will be the required result.

Now let us see some examples to comprehend the term standard deviation precisely.

Example:

Example 1:

Calculate the standard deviation for the given data

2, 1, 3, 5, 0, 4, 1, 3, 6,

Solution:

Step 1: Write down the given data in arranged form

1, 1, 2, 2, 3, 3, 4, 5, 6

Step 2: Calculate the average (mean) of the given data

x̄ = ∑x /n

x̄ = (1+1+2+2+3+3+4+5+6)/ 9

x̄ = 27/9

x̄ = 3

Step 3: Now we will perform steps 2 and 3 as illustrated in the following table.

x	(x - x̄)	(x - x̄)2
1	-2	4
1	-2	4
2	-1	1
2	-1	1
3	0	0
3	0	0
4	1	1
5	2	4
6	3	9

 

 

 

 

 

 

 

Step 4: Perform steps 4 and 5.

σ² = (∑x−x̄)²/n)

σ² = (4+4+1+1+0+0+1+4+9)/ 9

σ² = 24/9

σ² = 2.67 (Variance is the sum of the squared distances from the mean, divided by the number of data values.

Step 5: We take the square root on both sides.

σ = + 1.67 (Standard deviation can never be negative).

Example 2:

Calculate the standard deviation for the given data

4, 3, 1, 2, 6, 3, 2, 5, 1, 1, 2, 6

Solution:

Step 1: Write down the given data in arranged from

1, 1, 1, 2, 2, 2, 3, 3, 4, 5, 6, 6

Step 2: Find out the mean (average) of the given data

x̄ = (1+1+1+2+2+2+3+3+4+5+6+6)/ 12

x̄ = 36/12

x̄ = 3

Step 3: Now we will perform steps 2 and 3 as illustrated in the following table.

x	(x - x̄)	(x - x̄)2
1	-2	4
1	-2	4
1	-2	4
2	-1	1
2	-1	1
2	-1	1
3	0	0
3	0	0
4	1	1
5	2	4
6	3	9
6	3	9

 

 

 

 

 

 

 

 

 

Step 4: Perform steps 4 and 5.

σ² = (∑x−x̄)²/n)

σ² = (4+4+4+1+1+1+0+0+1+4+9+9)/ 12

σ² = 38/12

σ² = 3.17

Step 5: We take the square root on both sides.

σ = 1.78 which is the required result.

Summary:

In this blog, we have elaborated on the statistical term standard deviation, its definition, and the formula to find out SD. We have also discussed its important properties that are very useful for the computation of statistical problems and the study of statistical theory.